Understanding the K-Means Clustering Algorithm: A Comprehensive Guide
This article explores the discussion surrounding the K-Means clustering algorithm, a major element in machine learning and data science. Increasingly relevant to the field of search engine optimization (SEO), the K-Means concept forms the foundation for data segmentation and the creation of meaningful patterns. The article provides an eloquent explanation of the K-Means algorithm and its operational functionality within machine learning paradigms.
Additionally, the piece scrutinizes practical applications of the K-Means algorithm, especially its use in developing topic clusters from entity graphs - an innovation becoming increasingly crucial for businesses striving for superior SEO performance. After understanding the theory and application, the article navigates through challenges that professionals may encounter during implementation, specifically in a big data environment.
Furthermore, it sheds light on the diverse industries that widely use K-Means clustering, exemplifying the broad scope and relevance of the technique. Additionally, the innovative application of K-Means in information retrieval for the clustering of embedding chunks is elucidated.
Various factors contributing to algorithm performance are examined, and a comparative analysis with other clustering techniques is provided to broaden the readers' comprehension of K-Means' unique advantages and challenges.
The realm of machine learning is vast, filled with myriad algorithms operating silently behind the screens to orchestrate the digital world. Among these, the K-Means clustering algorithm stands out for its simplicity, versatility, and profound influence on the field of search engine optimization (SEO). This innovative method, though born out of mathematical theories and complex statistics, has a significant real-world impact, shaping consumer experiences across various industries.
This article delves into the intricacies of the K-Means algorithm, crafts a comprehensive understanding of its modus operandi, and critically examines its place in the larger picture of data analytics. It revolves around inquisitive explorations, offering readers insight into the
K-Means clustering algorithm's core and its applied aspects.
Firstly, the article provides a detailed explanation of the K-Means concept and working algorithm. Secondly, it seeks to understand its practical applications, with an emphasis on SEO and its utility in constructing efficient topic clusters within entity graphs. This aspect of K-Means holds particular importance in the current digital landscape, as businesses everywhere pivot toward a more data-driven approach to reach their objective faster and more efficiently.
The significance of K-Means in dealing with big data challenges is also discussed, as the digital universe continues to expand rapidly. Sequentially, we explore how K-Means Lends itself to the diverse industries, highlighting its relevance and adaptability. A particularly emerging field where K-Means is finding increasing application is in the clustering of embedding chunks, an area of modern information retrieval that the article covers.
The discussion progresses towards evaluating various factors affecting the K-Means algorithm's performance and accuracy, along with a comparison with other popular clustering algorithms. This perspective will enable the reader to gauge the unique advantages of K-Means, as well as its limitations. This comprehensive exploration of K-Means seeks to augment the reader's understanding and appreciation for machine learning, data science, and SEO.
What Is the Fundamental Concept Behind K-Means Clustering?
K-means clustering is one of the simplest yet most essential unsupervised machine learning algorithms, primarily utilized for data partitioning. The fundamental concept behind K-means clustering lies in its goal to subdivide a given data set into 'K' clusters, where each data point belongs to the cluster with the nearest mean.
In the context of machine learning, a 'cluster' is a group of data points that are more similar to each other than to those in other groups. The 'mean' refers to the centroid of each cluster.
To initiate the K-means clustering process, 'K' points are randomly chosen within the data set as initial centroids of the clusters. The algorithm then assigns each data point to the closest centroid based on a certain distance measure, most commonly the Euclidean distance. A new centroid is then calculated for each cluster, based on the average values of the data points within that cluster. This process of assigning data points and recalculating centroids is iteratively performed until the centroids' positions become stable, and the clusters remain unchanged.
One crucial aspect to note about the K-means clustering algorithm is that the value of 'K' must be predetermined. However, choosing the appropriate number of clusters is not always straightforward, as the optimal number often depends on the data set and the specific task at hand. Several methods, such as the Elbow method or the Silhouette method, can be employed to determine the most suitable 'K' value.
Another fundamental characteristic of K-means is its susceptibility to the initial selection of centroids. If the initial centroids are poorly chosen, the algorithm may converge to a local minimum rather than the global minimum, leading to suboptimal clusters. To mitigate this risk, the K-means++ algorithm, an extension of K-means, can be used. This approach ensures that the initial centers are distant from each other, which increases the likelihood of reaching the global optimum solution.
K-means clustering operates on the principle of minimization of within-cluster variance, often referred to as the inertia or within-cluster sum of squares criterion. The algorithm successively minimizes the sum of distances between the data points and their respective cluster centroids. Therefore, the k-means clustering algorithm forms tight clusters, and the data points in the same cluster are more similar than those in other clusters.
Despite its simplicity, K-means clustering provides robust results and has found extensive applications across various sectors, including computer vision, market segmentation, and search engine optimization (SEO). It aids in identifying homogenous groups within data, allowing for detailed insights, predictions, and tailored strategies.
In the context of SEO, for instance, K-means may facilitate creating meaningful topic clusters, aiding search engines in understanding content better, and thus improve a website's visibility. Therefore, mastering the K-means clustering algorithm is a desirable competency for professionals across numerous domains, from data science and marketing analytics to software engineering and SEO management.
The fundamental concept of K-means clustering lies in its definition as a partitioning algorithm, dividing data into K mutually exclusive clusters, wherein each data point belongs to the cluster with the nearest mean. This relatively simple technique can extract profound insights, making it a vital tool in the data scientist's arsenal.
How Does K-Means Clustering Algorithm Work in Machine Learning?
K-means clustering is a popular unsupervised learning algorithm known for its efficiency and simplicity in segmenting data into distinct categories or clusters based on variables or features.
This algorithm works by partitioning data into K distinct clusters, where every single data point belongs to the cluster with the nearest mean or centroid. The central lemma of the K-means algorithm falls under vector quantization that aids in data mining and statistical data analysis.
At the inception of the algorithm, 'K' centroids are chosen at random from the dataset to form initial clusters. Next, each of the remaining data points is assigned to the nearest centroid based on a distanced function. In most cases, the Euclidian distance is used because of its simplicity and efficiency.
Following this, a recalculation ensues, wherein the centroids of the newly formed clusters are recalculated. This is done by computing the mean values of all the data points of each cluster. This results in a shifting, and sometimes considerable displacement, of the centroid to a new location. Consequently, the data points are reassigned again to the closest centroid, which might or might not change its cluster assignment.
This iterative process of reassignment and recalculation continues until the algorithm converges. The converging criterion is met when the centroids no longer move, or the assignments of data points to clusters remain constant, effectively meaning the algorithm has found the most suitable grouping for the data.
While the implementation of K-means clustering is relatively straightforward, one of its main complexities lies in determining the optimal number of clusters 'K'. This is where techniques like the Elbow Method are often used to evaluate and select the right number of clusters, ensuring the machine learning algorithm captures patterns in the data most effectively.
Another fundamental aspect of K-means is its sensitivity to the initial starting conditions. Different random starting points might generate different results. To resolve this, the algorithm can be run several times with different initial positions, usually providing a more reliable final cluster classification.
Despite these complexities, the K-means clustering algorithm is immensely beneficial in machine learning. Its popularity comes from its scalability and efficiency, especially with large, high-dimensional datasets. Its ability to reveal structure within data makes it an essential tool in exploratory data analysis and an excellent pre-processing step for other machine learning algorithms.
From customer segmentation, document clustering to image recognition and anomaly detection, K-means clustering has found applications in diverse fields, making complex data manageable, understandable, and usable. Its ability to transform myriad points into coherent groups helps machines, and thus people, to make better sense of the world and the vast amounts of data it produces.
The K-means clustering algorithm is a powerful unsupervised machine learning technique that works by grouping data into 'K' clusters based on similarity and distance from centroids. Despite its simplicity, it uncovers profound insights in data, paving the way for smarter decisions, improved efficiencies, and the discovery of patterns that might never have been obvious otherwise.
How Can K-Means Be Used in the Creation of Topic Clusters in Entity Graphs?
Topic clustering, a method of categorizing and structuring content, is poised to transform the field of SEO.
It allows for a better understanding of a website's content, resulting in improved relevancy and discoverability within search engine results. K-Means, a popular clustering algorithm, plays a critical role in creating topic clusters, effectively harnessed in entity graphs.
Entity graphs are a type of knowledge graph representing the relationships between various entities within a particular domain, thereby assisting in revealing significant semantic links. It visualizes how topics interconnect and interact, providing a microcosm of complex data structures.
The K-Means algorithm segmentizes data into clusters based on attributes, aiming to minimize intra-cluster distance while maximizing inter-cluster distance. The number of clusters ('K') is empirically decided to balance detail with manageability. In the context of entity graphs, the 'distance' can equate to how closely related two topics are semantically. These clusters, established based on relevancy, can then form the basis of topic clusters within an entity graph.
The first step in using K-Means to create topic clusters involves determining 'K' – the number of clusters. SEO professionals must gain an understanding of the knowledge area to make informed decisions about the number of topic clusters they aim to form.
Next, the algorithm initiates by randomly assigning entities to clusters. It then calculates the centroid – or the mean value – of each cluster. Following this, each entity, representing different topics, is reassigned to the cluster with the nearest centroid. This process continues iteratively until the algorithm converges to a point where reassignment no longer alters the clusters' centroids.
The resulting clusters correlate with topics within the entity graph. Entities within each cluster share a closer relationship, demonstrating stronger associations, than entities allocated to different clusters. Therefore, these clusters can form topic clusters, structuring content within the domain.
This use of K-Means for topic clustering within entity graphs brings several advantages. Firstly, it helps search engines understand and index content more accurately, enhancing the website's SEO. Additionally, it can identify key topics and subtopics dynamically, allowing users to find the most relevant content more easily. Marrying K-Means with entity graphs also enables topical authority and deeper context to content, which can be an essential tool for content and digital marketing specialists in the planning and execution of data-driven strategies. The application of topic clusters created by K-Means in entity graphs enhances user navigation and improves user experience as a whole.
Interestingly, the future may see enhancements to the process of K-Means clustering, enabling dynamic adjustment of 'K' as the knowledge domain evolves, thereby maintaining the topical relevancy of the clusters. As the digital world advances, combining these clustering and graphing techniques remains an exciting and powerful tool in SEO, improving website optimization, and facilitating content discoverability.
What Are the Practical Uses of K-Means Clustering in Data Analysis?
K-Means clustering is a versatile algorithm with a variety of practical applications in the realm of data analysis.
Its primary function is to segregate datasets into distinct clusters based on shared characteristics or features, enabling organizations to rationalize their data and derive actionable insights. Below are some of the most compelling use cases of K-Means clustering in data analysis.
Firstly, K-Means shines in the arena of customer segmentation, a critical part of modern marketing strategies. Businesses use K-Means to segregate their customer basins into distinctive groups based on purchasing behavior, preferences, demographic information, and other factors. These segmented clusters enable targeted marketing and promotional campaigns, personalized product recommendations, and more nuanced customer service approaches - all of which can considerably enhance customer engagement and boost sales metrics.
Another mainstay application of K-Means lies in anomaly detection - the identification of data points that deviate from usual patterns. This deviation could signal fraudulent activity in credit card transactions, a cyber breach in network security, or faulty performance in a mechanical system. K-Means clustering identifies such anomalies by grouping normal operations into clusters and highlighting data points that fall outside these parameters.
Moreover, K-Means can be used effectively in image segmentation and compression. By identifying and clustering similar pixel values, the algorithm can remove redundant information, leading to more efficient storage and quicker processing times. This use-case is particularly popular in fields like digital media, online marketing, and computer vision.
Saliently, K-Means plays a key role in the field of document clustering or text mining. It can cluster documents or articles into groups based on similar themes or topics. This feature is invaluable in SEO, where the creation of topic clusters from entity graphs can provide a more organized, user-friendly website architecture, boosting both user experience and search engine rankings.
K-Means also finds application in the field of bioinformatics. Genome sequencing and gene expression data are known for high dimensionality, making data analysis quite challenging. K-Means clustering is capable of reducing these complex datasets into manageable clusters, thus facilitating more efficient data exploration and debugging.
Additionally, K-Means clustering is instrumental in spatial data analysis, commonly used in geography and meteorology. By clustering geographical data into different regions, the algorithm allows for effective land-use planning, weather pattern analysis, and even crime tendency mapping in different locales.
Lastly, another interesting application is in the field of search engine result refining. Here, K-means can help cluster search results into different categories, allowing users to navigate through results more efficiently.
These are just a handful of the myriad ways K-Means clustering is used in data analysis. Whatever the industry – be it healthcare, finance, retail, or technology – K-Means has paved its way into the heart of data analysis, providing valuable insights and influencing strategic decisions. Its adaptability, simplicity, and precision make it a robust tool, capable of dealing with the increasingly complex landscape of big data. As data continues to grow exponentially, the relevance and necessity of effective data clustering methods like K-Means only stand to increase.
How to Optimize the Number of Clusters in a K-Means Algorithm?
The K-Means clustering algorithm is effective for segmenting data, but determining the optimal number of clusters is a fundamental aspect that can decisively influence your algorithm's performance and the insights derived from it.
Here are valuable strategies that can help optimize the number of clusters in a K-Means algorithm.
- Elbow Method: As one of the most popular techniques, the Elbow Method essentially involves running the K-Means algorithm several times over a range of values for 'k' (the number of clusters). In each iteration, the variance is calculated, indicating how much each data point deviates from its cluster centroid. The variance typically decreases as 'k' increases because having more clusters means data points are closer to centroids. The ‘elbow point’, or the point on the graph where increasing 'k' doesn't significantly reduce the variance, is considered the optimal number of clusters.
- Silhouette Analysis: This method measures how close each data point in one cluster is to the points in the neighboring clusters. Silhouette coefficients can vary between -1 and 1. A high value implies that data points are well-matched to their own cluster and poorly linked to neighboring clusters. For the optimal number of clusters, the average silhouette value will be at a maximum.
- Gap Statistic: The gap statistic compares the total intracluster variation for different values of 'k' with their expected values under null reference distribution of the data. The optimal number of clusters is usually where the gap statistic reaches its maximum.
- Cross-validation Method: Often used in machine learning algorithms, this method involves partitioning the dataset into a set of 'k' subsets. The K-Means algorithm is performed 'k' times, each time using a different subset as a test set and the remaining data as a training set. The 'k' results are averaged to get a final value. The optimal number of clusters corresponds to the solution with the smallest error on the unseen test data.
- AIC and BIC Measures: These are statistical methods used to evaluate the model's goodness of fit and simplify the trade-off issue between bias and variance in model testing. A lower value of both measures indicates a better model. Therefore, the optimal number of clusters for K-Means can be the one that minimizes AIC and BIC.
Remember that each method has its strengths and weaknesses and is best suited for specific kinds of problems. It's crucial to understand your data and the requirements of your specific task to choose the most appropriate method. Furthermore, you may need to standardize your data before executing the K-Means algorithm, especially when dealing with variables of different units.
Ultimately, correctly identifying the optimal number of clusters plays an integral role in obtaining valuable insights from your data. It aids in understanding the underlying structure of the data, thereby assisting in making informed, data-driven decisions. Keep in mind that improving machine learning models is often an iterative process, so don't be discouraged if you don't get it perfect on the first try.
What Challenges Arise When Implementing K-Means Clustering in Big Data?
The implementation of the K-Means clustering algorithm brings plenty of opportunities for extracting value from big data, but it is not without challenges.
The massive volumes, high velocity, and significant heterogeneity of big data can introduce complexities and difficulties that need to be adequately addressed in order for the K-Means clustering to be effective.
One of the significant challenges is the issue of scalability. K-Means algorithm, by its nature, requires iterative computations to find the optimum clusters. As the volume of data increases, the processing demands significantly surge. A large dataset means more data points to compute distances, which can be computationally expensive and time-consuming for regular computational systems. Consequently, the algorithm's effectiveness and speed may be hampered, as it could take inordinate amounts of time to arrive at the optimal centroids, hindering the real-time analysis of data.
The initial selection of centroids is a critical aspect of the K-Means algorithm, often posing a challenge. The outcome of the algorithm can be profoundly impacted by the starting locations of the centroids. Poorly chosen initial points might lead to suboptimal clustering or slow convergence. With big data’s complexity, appropriately selecting these initial points becomes increasingly difficult, and the risk of suboptimal results magnifies.
As K-Means is a distance-based algorithm, it can struggle with high-dimensional big data. As the number of dimensions in a dataset increases, distinguishing between close and far becomes blurred – a phenomenon known as the curse of dimensionality. This concern makes it hard for the algorithm to effectively form distinct clusters, potentially impacting the efficiency of the analysis and data interpretation.
The K-Means algorithm often works on the assumption that clusters are of similar size, which may not be the case in diverse datasets common in big data. This assumption can lead to problems with biased clustering, where clusters of larger sizes are favored over smaller ones. Similarly, K-Means is also less effective with non-spherical clusters because it minimizes variance and not a metric that would allow more flexibility in cluster shapes.
While K-Means requires predefined cluster number (k), deciding the 'k' value a priori is not always straightforward, particularly in big data scenarios where hidden structures are unknown. Misestimation of this parameter can lead to significantly ineffective clustering.
Addressing these challenges often calls for the adaptation of the traditional K-Means algorithm. Algorithms like K-Means++, Mini Batch K-Means, or other modified versions that account for big data's distinctive features have been developed. Furthermore, distributed and parallel computing frameworks have also been used to tackle the data scalability issue.
While the K-Means algorithm has promising potential for big data analysis, several challenges need to be overcome. Developing appropriate strategies to deal with these constraints is crucial to leverage the full potential of the K-Means clustering algorithm in big data.
Which Industries Commonly Use K-Means for Data Clustering and Why?
K-Means clustering has found its place in an impressive variety of industries as a sought-after method for data segmentation and exploratory data analysis.
The algorithm's adaptability, simplicity, and proficiency at identifying patterns render it an invaluable asset in accumulating data and harnessing it to drive business decisions.
Finance represents one of the key industries where K-means plays an integral role, utilized in portfolio management, risk analysis, and customer segmentation. Investment firms employ
K-means to segregate stocks into distinct portfolios based on patterns and correlations in historical price data, enabling optimal asset allocation. Credit scoring and risk profiling employ
K-means to group customers based on similar credit histories, affording better risk management.
Healthcare is another sector drastically transformed by K-means clustering. It helps in effective patient categorization, disease prediction, and aids in the detection of health patterns and anomalies. Hospitals can categorize patients with similar symptoms, thereby predicting potential illness and personalizing patient care for improved outcomes.
In the retail industry, K-Means contributes significantly to customer segmentation and tailoring personalized marketing strategies. By clustering customers based on purchasing behavior, preferences, and demographics, retailers can design customized promotional offers to boost sales. This targeted approach increases customer satisfaction and reduces resource wastage in blanket marketing approaches.
Telecommunications companies employ K-means to enhance their customer churn prediction models. By segmenting customers based on usage patterns, feedback data and customer demographics, telecom companies can preemptively identify potential churn risks, enabling them to implement necessary retention strategies and improve their customer service.
K-Means is also a firm favorite among tech titans in the field of search engines and social networking. Google, for example, uses K-Means for clustering vast volumes of data for its news propagation and things like keyword, topic, and embedding clusters. Social media companies use the algorithm for segmenting user profiles and serving personalized content thereby enhancing user experience and retention rate.
K-Means has also found its place in academia and research, extensively used in exploratory data analysis. Educational institutions and stakeholders use algorithm-based clustering for segregating students based on their performance, learning styles and behaviors, helping instructors to individualize pedagogical strategies. It also aids academic researchers in segregating data into meaningful subsets for a more targeted analysis.
Lastly, in the realm of agriculture, K-Means has great promise in precision farming. By analyzing satellite imagery and sensor data, the algorithm can identify patches with similar crops or those affected by similar diseases, enabling farmers to implement targeted farming strategies and manage resources optimally.
K-means clustering has emerged as an extraordinarily versatile tool in a multitude of industries. Its unique capability to find meaningful patterns in data proves pivotal in uncovering hidden insights and shaping growth strategies. With the pace of data generation increasing steadily, K-Means’ importance across industries is ripe to rise further.
How Does K-Means Apply to the Clustering of Embedding Chunks in Information Retrieval?
In the fascinating realm of Information Retrieval (IR), K-Means clustering expands its prowess in the newly advanced technique of embedding chunk clustering.
This approach moves beyond traditional keyword-based queries, enabling more nuanced, context-aware information retrieval that significantly boosts the quality of search results.
Embedding chunk clustering refers to the grouping of small chunks of text data, or 'chunks,' based on their semantic similarity represented through numerical vectors or embeddings. An embedding is a multi-dimensional representation of the data which places data chunks with similar features closer while distancing ones with contrasting attributes. The key lies not just in the chunks' literal meaning but more in the context of their usage, thus bringing previously disparate pieces of data close together on the basis of shared or related meanings.
The K-Means algorithm fits brilliantly into the practice of chunk embeddings, offering a systematic approach to cluster these embeddings into distinct groups where intra-cluster similarity is high, and inter-cluster discrepancy is maximized.
In brief, the algorithm first assigns an arbitrary centroid value to each cluster. Then it computes the distances between the embeddings and these centroids, attaching each chunk to the nearest centroid, consequently forming clusters. Following this, the centroid values are recalculated based on the current members of each cluster. This process is iterated until there are no changes in the centroid values, arriving at the optimal cluster configuration.
When the K-Means clustering is applied to embedding chunks in IR, a machine learning model can evaluate and understand the context and nuanced meaning of different chunks in a dataset, regardless of their size. This context-based understanding helps to group together relevant data chunks. For instance, a sports article and a health column explaining the benefits of regular exercise might end up in the same cluster due to similarity in context, despite having different themes.
The natural language understanding gained through this clustering process goes a long way towards making search results richer, more relevant, and intuitively aligned with the user's intent. In a broader view, it paves the way towards a more semantic web, where the nuance and context of language are honored and leveraged. Users gain from the superior quality of results, and service providers enhance their user satisfaction, retention, and operational efficiency.
K-Means based clustering of chunk embeddings also finds vital use in document summarization, sentiment analysis, and machine translation, enriching the human-machine communication. While techniques like Word2Vec or BERT serve to create meaningful embeddings, K-Means acts as a technique to effectively organize these embeddings.
The use of K-Means for clustering embeddings, however, is not without challenges. The algorithm's sensitivity to the initial positioning of centroids and problems handling clusters of different sizes and densities are some issues to be mindful of. Choosing the optimal number of clusters (K) is another challenge that influences the outcome.
The application of the K-Means clustering algorithm to clustering chunk embeddings in IR signifies an impactful stride towards more intelligent, context-aware information retrieval systems, leading to enhanced user experiences. Benefiting both end-users and service providers, this strategy combines the best of mathematical algorithms and natural language processing, mapping the way forward for a nuanced understanding and application of data in the digital realm.
What Factors Can Impact the Performance and Accuracy of K-Means Clustering?
Several factors can significantly impact the performance and accuracy of the K-Means clustering algorithm.
Recognizing these factors is crucial in obtaining optimal results when using this popular machine learning tool.
The initial selection of centroids in the K-Means algorithm can greatly influence the result. K-Means clustering begins with the random or heuristic selection of k-points as initial centroids. The algorithm’s effectiveness can vary based on these initial selections. If they are poorly chosen, the algorithm may not converge optimally, yielding inaccurate clusters. A poor initial choice can cause the algorithm to fall into local optima rather than reaching the global optimal solution. Techniques like K-Means++ can be used to overcome this limitation by ensuring smarter initialization of centroids.
The value of K (number of clusters) directly affects the output. Choosing an appropriate K value is imperative for achieving accurate results. A wrong estimation can lead to underfitting or overfitting of data. Several techniques like Elbow Method and Silhouette Analysis are often used to determine an appropriate K value.
Another factor to consider is the quality and nature of the dataset. The presence of outliers can significantly impact the K-Means algorithm, potentially skewing the centroids and producing non-representative clusters. Moreover, K-Means assumes that clusters are spherical and balanced, which might not always be the case in real-world data.
The dimensionality of the dataset also influences the effectiveness of the K-Means algorithm. As the number of dimensions (features) increases, the chances of two points being closer become increasingly rare, a phenomenon known as the curse of dimensionality. This can hinder the algorithm's performance and accuracy significantly.
Furthermore, the preprocessing of data can significantly impact the results. Missing data, if not handled well, can distort the results of the algorithm. Similarly, variable scales should be carefully considered and normalized to ensure each variable carries an equal weight when calculating distances between data points.
The performance and accuracy of K-Means can also be affected by the underlying metric used to measure the 'distance' between data points. The most common metric used is Euclidean distance, but depending on the data type and domain, other distance measures like Manhattan, Minkowski, or cosine similarity may be more appropriate.
The algorithm's sensitivity to the order of the data points can impact results. Running the algorithm on the same data but in a different order can lead to contrasting results due to the incremental update of the cluster's centroid.
While the K-Means clustering algorithm is a powerful tool in machine learning, it is essential to understanding its sensitive nature towards several factors. By carefully considering these factors, one can leverage K-Means clustering more effectively to solve complex problems in data science and SEO optimization.
What Are the Differences between K-Means and Other Clustering Algorithms?
Machine learning, an influential subset of artificial intelligence, comprises numerous unique clustering algorithms that help interpret and make sense of the vast datasets we encounter daily. At the forefront of these algorithms is K-Means, a simple yet versatile clustering algorithm.
But how does it distinguish itself from the others?
The K-Means algorithm is a procedure that divides a set of n-dimensional data into K non-overlapping subgroups or clusters, thereby simplifying big data analysis. As its defining feature, K-Means is a centroid-based algorithm. This means it organizes data into clusters around a central location point (centroid). It calculates the distances from data points to the centroids to determine their cluster memberships.
On the other hand, there are other clustering algorithms with different approaches and advantages. Take, for example, the Hierarchical Clustering Algorithm. Unlike K-Means, this algorithm does not require pre-specifying the number of clusters. It creates a tree of clusters called a dendrogram, allowing the user to choose the number of clusters later by "cutting" the dendrogram at the appropriate level. Here, clusters have parent-child relationships and may share data points, a dynamic wholly absent in K-Means.
Another prominent clustering algorithm is DBSCAN (Density-Based Spatial Clustering of Applications with Noise). This algorithm groups together points that are packed closely together (points with many nearby neighbors), marking points that lie alone in low-density regions as noise or outliers. It means DBSCAN can identify and handle noise, and can find arbitrary shaped clusters, which is not possible with K-Means.
Model-based algorithms, such as Gaussian Mixture Models (GMM), assume data are generated from a mixture of finite Gaussian distributions with unknown parameters. Unlike K-Means that assigns a data point to one and only one cluster, GMM assigns a probability to each point belonging to each cluster.
The Spectral Clustering algorithm, which operates in a wholly different domain compared to K-Means. This algorithm uses the eigenvalues of the similarity matrix to reduce the dimensionality of the dataset before clustering in a lower-dimensional space. It makes Spectral Clustering algorithm especially useful for non-convex datasets, something that K-Means could not handle.
The Mean-Shift Clustering algorithm, unlike K-Means, does not require the user to specify the number of clusters. Instead, it uses a kernel (a weighting function) to navigate the data points towards the densest part of the data cloud and find the number of clusters automatically.
While K-Means clustering shines in its simplicity and efficiency in segregating high-dimensional data, other clustering algorithms offer different perspectives and techniques to approach the challenge of data segregation. It's crucial to consider these differences and the nature of the data at hand when choosing the optimum clustering algorithm for a given task. Understanding the uniqueness of K-Means compared to other clustering algorithms enables us to harness its potential more effectively, thereby deriving valuable insights from our data.
How Market Brew Uses K-Means to Model Topic Clusters and Embedding Clusters
Among the variety of machine learning tools and technologies at its disposal, Market Brew has employed the K-Means clustering algorithm to streamline its SEO techniques, particularly in the modeling of topic clusters and embedding clusters.
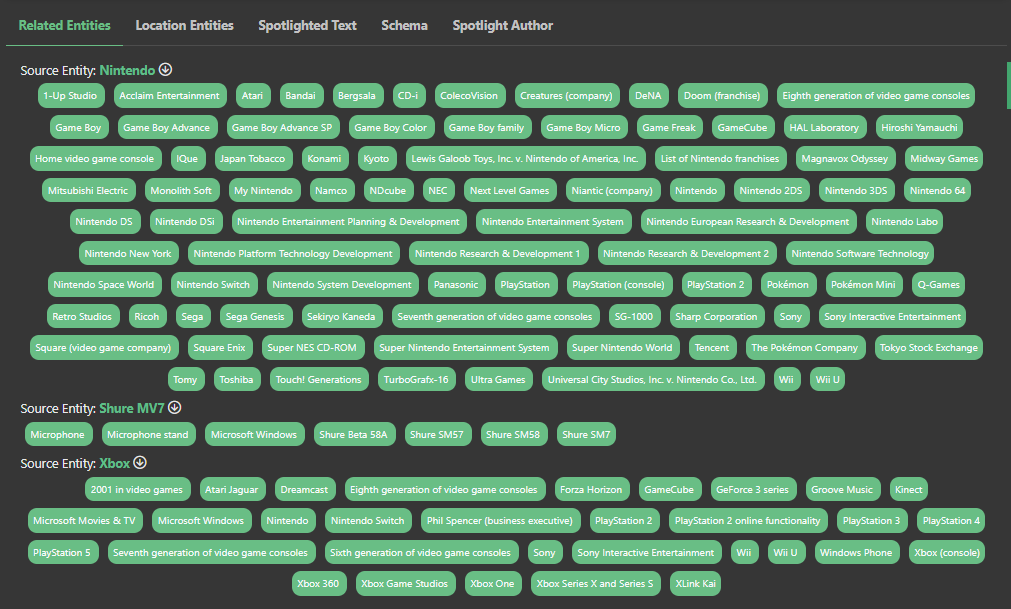
The use of K-Means for developing topic clusters in Market Brew's approach is specifically designed to model the way Google views its entity graph. Market Brew's topic cluster algorithm models this by identifying entities sharing the same parent entities on a page. This process is essential as these entities provide the vital context that a search engine model needs to understand the content better, subsequently providing a more precise picture of how Google works.
By using K-Means clustering, Market Brew identifies these shared parent entities and then isolates the top three entities that the page is primarily about. This focused identification of the key topics on-page enables SEOs to understand how a search engine views the entity structure of a given page.
Effectively, this approach allows users to create tightly linked groups of related content, which boosts the visibility and accessibility of their information on search engines. When search algorithms understand the clusters of entities created through K-Means, they can better comprehend the contextual relevance of the content. This increases the likelihood of a favorable SERP (Search Engine Results Page) position, enhancing visibility, and organic traffic.
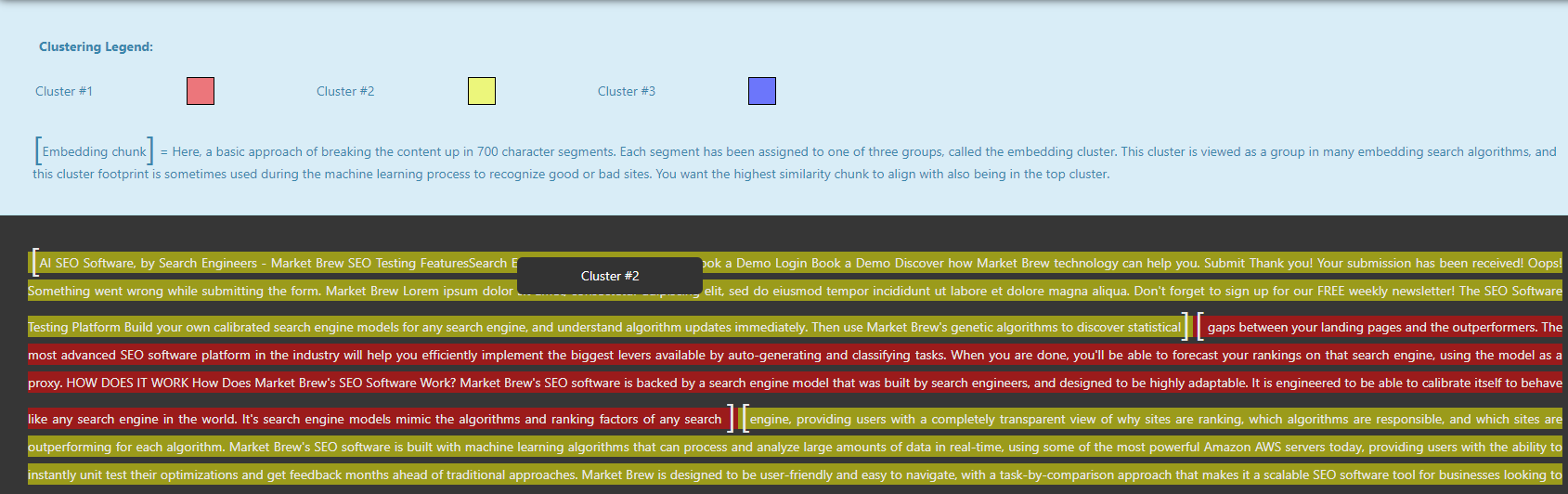
In addition to topic clustering, Market Brew applies K-Means clustering in the innovative area of embedding chunks. Here, the content is broken up into segments, in a similar way to the Sentence-BERT approach, each comprising approximately 700 characters. Each of these segmented chunks is assigned to one of three embedding clusters through the K-Means algorithm.
The choice of cluster for each chunk depends on the meaning and relevance embedded within the piece of content.
This clustering of embedding chunks serves multiple purposes.
Firstly, it simplifies the search algorithm by categorizing the content into manageable and comprehensible groups.
Secondly, the K-Means generated embedding cluster footprint can be utilized during the machine learning process to train algorithms on identifying high-quality or poor-quality sites. Instead of assessing the entire site in one go, the algorithm can look at these embedding clusters and understand the site's quality and relevance.
Ideally, the highest similarity chunk should align with being in the top cluster, showing that the most relevant information is also the most accessible and easily understood.
Market Brew's exploitation of the K-Means clustering algorithm showcases the potential of machine learning in advancing SEO practices.
Through effective modeling of topic clusters and embedding clusters, Market Brew's A/B testing platform allows users to see exactly which types of topic clusters and embedding clusters Google prefers, by singling out the specific landing pages that score the highest for these algorithms.
Ready to Take Control of Your SEO?
See how Market Brew's predictive SEO models and expert team can unlock new opportunities for your site. Get tailored insights on how we can help your business rise above the competition.
Schedule a demonstration today via our Menu Button and Contact Form to discover how we engineer SEO success.
You may also like
Guides & Videos
Others
Boost Your Conversion Rates with SEO Best Practices
Guides & Videos
SEO Internal Linking Detailed Guide
History


