The Role of Cosine Similarity in Vector Space and its Relevance in SEO
As the digital world continues to expand, there is an increasing need to quantitatively measure and understand the similarity between data points. This is particularly important for Search Engine Optimization (SEO), where the relevance between entities significantly influences ranking algorithms.
This paper focuses on Cosine Similarity, a robust and widely-used similarity measure based on the angle between two vectors. It is a critical tool used in several applications ranging from information retrieval, text mining, data science, and digital marketing, among others. The range of values for Cosine Similarity, as well as its interpretation, will be thoroughly discussed.
In addition, the advantages and potential challenges of using Cosine Similarity will also be scrutinized, illustrating the need for careful data preprocessing and understanding of its limitations. This paper will also shed light on the variations or adaptations of Cosine Similarity that find relevance in specific industry domains, emphasizing its versatility and importance in driving search engine results.
In the realms of machine learning, data analysis, and SEO, understanding vector similarity metrics such as Cosine Similarity, is pivotal. This paper elucidates the concept of Cosine
Similarity, its mathematical underpinnings, and the role it plays within the landscape of vector space. Comparative analysis with other popular metrics like Euclidean Distance and Jaccard Similarity is utilized to highlight the uniqueness of Cosine Similarity.
Real-world applications, particularly in text data analysis, are also explored. Subsequently, the potential challenges or limitations when applying Cosine Similarity in certain scenarios are discussed.
The article ends by suggesting some preprocessing data techniques to improve the efficiency of Cosine Similarity in any given application, along with a look at its variations or adaptations in specified domains or industries.
What Is Cosine Similarity, and How Does It Measure Similarity Between Two Vectors?
Cosine similarity is a mathematical measure commonly used in machine learning and natural language processing to assess the similarity between two vectors. It specifically quantifies the cosine of the angle between these vectors, providing a measure of their orientation rather than their magnitude. This approach is particularly useful in scenarios where the magnitude of the vectors is less relevant, and the focus is on the direction or alignment of the data.
Vectors, in this context, refer to mathematical entities that represent sets of values. These values could represent anything from word frequencies in a document to pixel intensities in an image. The vectors are essentially arrays of numerical values, and the cosine similarity metric is employed to determine how similar or dissimilar these vectors are in terms of their orientation.
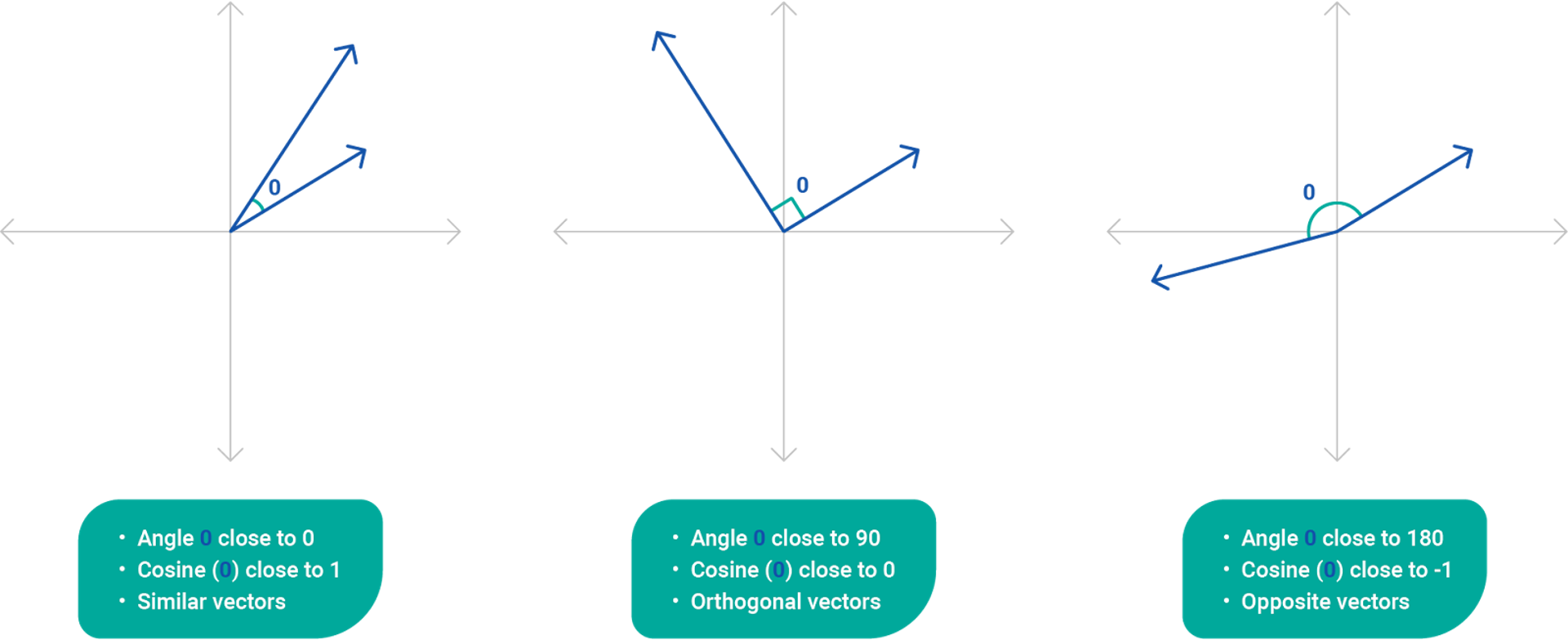
The cosine similarity measure ranges from -1 to 1, with -1 indicating completely opposite directions, 0 representing orthogonality (perpendicularity), and 1 signifying identical directions.
The computation is based on the dot product of the vectors, a mathematical operation that multiplies corresponding elements of the vectors and sums up the results.
The formula for cosine similarity between two vectors, A and B, is expressed as follows:
Cosine Similarity(A, B) = (A · B) / (||A|| * ||B||)
Here, A · B denotes the dot product of vectors A and B, while ||A|| and ||B|| represent the Euclidean norms of vectors A and B, respectively.
To illustrate the concept with a simple example, consider two vectors in a two-dimensional space: A = [3, 4] and B = [1, 2]. The dot product is calculated as A · B = (3 * 1) + (4 * 2) = 11.
The Euclidean norms are ||A|| = sqrt(3^2 + 4^2) = 5 and ||B|| = sqrt(1^2 + 2^2) = sqrt(5).
Plugging these values into the cosine similarity formula, we get:
Cosine Similarity(A, B) = 11 / (5 * sqrt(5))
This numerical result represents the cosine similarity between the two vectors.
The advantages of using cosine similarity lie in its ability to capture the directional aspect of the data, while being robust to changes in vector magnitudes. This property makes it particularly valuable in natural language processing tasks, such as document similarity analysis and information retrieval. In these applications, vectors often represent document embeddings or word representations, and cosine similarity helps identify the similarity in meaning or content between different texts.
One of the key applications of cosine similarity is in document similarity analysis. By representing documents as vectors based on word frequencies or embeddings, cosine similarity enables the comparison of documents in a meaningful way. For instance, in a search engine, when a user queries a document, the system can use cosine similarity to retrieve documents that are most similar in content.
Can You Explain the Mathematical Formula for Cosine Similarity and Its Significance in Vector Space?
The cosine similarity measure ranges from -1 to 1, with -1 indicating completely opposite directions, 0 representing orthogonality (perpendicularity), and 1 signifying identical directions. The computation is based on the dot product of the vectors, a mathematical operation that multiplies corresponding elements of the vectors and sums up the results.
The mathematical formula for cosine similarity encapsulates a simple yet powerful concept with widespread applications in vector space. Its significance lies in its ability to measure the similarity between vectors while disregarding their magnitudes, making it a versatile tool in information retrieval, natural language processing, and machine learning. The metric's robustness to varying vector lengths and its geometric interpretation enhance its utility, contributing to its prevalence in diverse fields.
The formula for cosine similarity between two vectors, A and B, is expressed as follows:
Cosine Similarity (cos(θ)) = (A · B) / (||A|| * ||B||)
Here, (A · B) denotes the dot product of vectors A and B, while (||A|| * ||B||) represent their respective Euclidean magnitudes. The numerator, (A · B), captures the contribution of each element in both vectors, signifying the similarity in directionality. The denominator, (||A|| * ||B||), normalizes the result by the product of their magnitudes, emphasizing the independence of the vectors' lengths.
The significance of the cosine similarity metric lies in its ability to quantify the similarity between vectors irrespective of their magnitudes. This makes it particularly valuable when dealing with high-dimensional data where the magnitude of vectors might not be a reliable indicator of similarity. The cosine similarity ranges between -1 and 1, with 1 indicating identical vectors, 0 representing orthogonality, and -1 denoting vectors in opposite directions.
In vector space, documents or texts are often represented as vectors, with each dimension corresponding to a term or feature. By employing cosine similarity, one can assess the resemblance between these vectors, enabling tasks such as document retrieval, clustering, and classification. For instance, in information retrieval, cosine similarity helps identify documents with similar content, aiding search engines in delivering relevant results.
Additionally, cosine similarity is robust to changes in vector length, making it advantageous in scenarios where the magnitude of the vectors may vary. This characteristic proves beneficial in natural language processing applications, such as text clustering and document categorization, where the length of texts can differ significantly.
Moreover, cosine similarity facilitates the comparison of vectors in a geometric sense, as it measures the cosine of the angle between them. When the vectors are similar, the cosine of the angle is close to 1, indicating a small angle and high similarity. Conversely, if the vectors are dissimilar or orthogonal, the cosine similarity approaches 0, reflecting a larger angle and diminished similarity.
How Is Cosine Similarity Different from Other Similarity Metrics, Such as Euclidean Distance or Jaccard Similarity?
Cosine similarity, Euclidean distance, and Jaccard similarity are all advanced mathematical metrics that are used in machine learning, data analysis, and other applications to quantify the degree of similarity or dissimilarity between two entities, such as two vectors or two data sets. Despite their shared purpose, these three metrics function very differently and suit certain types of data or situations more than others due to their unique mathematical properties.
Cosine similarity measures the cosine of the angle between two non-zero vectors. The cosine similarity of identical vectors is 1, while the cosine similarity of orthogonal vectors is 0. Unlike
Euclidean distance and Jaccard similarity, cosine similarity is not concerned with the magnitude of the vectors, only the angle between them. This makes it particularly useful in text mining and information retrieval to compare the similarity between documents or texts represented as term frequency vectors. Using cosine similarity, a large document can be considered similar to a smaller document if they share the same orientation, regardless of their lengths.
Euclidean distance, or L2 distance, quantifies the straight-line distance between two points in space. It is sensitive to the magnitude of the vectors and can change dramatically with scaling or translation, unlike cosine similarity. Euclidean distance is widely used in clustering problems and works well with dense data sets where all attributes have the same units of measurement.
However, it may not work well with high-dimensional data due to the 'curse of dimensionality'.
Jaccard similarity, on the other hand, is a measure of the overlap between two sets. It is defined as the size of the intersection divided by the size of the union of two sets and produces a value between 0 (no overlap) and 1 (perfect overlap). Jaccard similarity is best used with binary or categorical data, as well as sparse data sets where the absence of an attribute is as important as its presence. It does not consider the magnitude or orientation of the vectors and is not suitable for numerical data or data that can take a range of values.
In essence, cosine similarity, Euclidean distance, and Jaccard similarity provide different ways to quantify similarity based on different features of the data – the angle between vectors, the straight-line distance between points, or the overlap between sets, respectively. The right similarity metric to use depends on the nature of the data and the specific requirements of the analysis or application.
In What Applications Is Cosine Similarity Commonly Used?
Cosine similarity is a critical mathematical tool that finds its application across various domains because it's a measure of determining the substantive similarity between distinct objects or documents. While considering the angle between vectors representing these objects in high-dimensional spaces, the cosine similarity quantifies their similarity regardless of their sizes.
This concept is extensively used in fields like data science, machine learning, information retrieval, and natural language processing (NLP) as it leverages the concept of multi-dimensionality.
One of the common applications is in text mining and document comparison. For example, in Search Engine Optimization (SEO), cosine similarity is used in the semantic matching process to draw connections between a user's query and potential search results. In SEO, the similarity between the keywords in the searcher's query and the content of a webpage provides a measure used to rank the page in search engine results following specific algorithms.
Secondly, it is also widely used in content-based recommendation systems. Let's consider an e-commerce platform where millions of items are available. To recommend an item to a user that is closely related to the items previously bought or viewed by the customer, cosine similarity assessment is used. It helps determine similar products by comparing features or properties of products.
In the field of machine learning, cosine similarity is used in cluster analysis. It helps segregate vast datasets into distinct groups or clusters based on their similarity. This application is user-oriented and depends predominantly on the content.
Furthermore, in NLP, cosine similarity is indispensable. For instance, it helps identify plagiarism by comparing the essay or article with a collection of other works. The more similar the work, the higher the chance it has been plagiarized. Similarly, it determines the relevance of information to the topic in question when sorting data or filtering out irrelevant information.
In digital image processing, cosine similarity is used for image comparison and recognition. A target image is compared with a library of known images, and the one with the highest cosine similarity score is tagged as the most similar. This application is often employed in facial recognition systems or reverse image search engines.
Moreover, in bioinformatics, cosine similarity allows classifying genes with similar traits or identifying similar protein sequences, playing a crucial role in understanding genetic behaviors and disease treatment research.
How Does the Angle Between Two Vectors Influence Their Cosine Similarity?
The concept of the angle between two vectors is salient in various scientific fields, including Search Engine Optimization (SEO) for indexing and ranking web page content by search engines. Specifically, this concept is integral in the measurement of the cosine similarity between vectors, a critical tool in determining the relevance of content within the SEO context.
Cosine similarity is a metric used to measure how closely related two vectors are to each other based on their same dimensions. This metric represents the cosine of the angle between two vectors; the smaller the angle, the closer to one the cosine value, indicating a higher similarity. SEO utilizes the principle of cosine similarity in "vector space models" which are extensively used in information retrieval, a branch of SEO.
In terms of SEO, these vectors ideally represent documents or pieces of text (containing keywords), with the dimensions representing specific terms or phrases. It helps in assessing the similarity between documents or, more importantly, the relevance of a document to specific search terms. If the angle is small (close to 0°) i.e., vectors are very similar, the cosine score is close to 1, indicating that the document is highly relevant to the search terms. Conversely, if the vectors are dissimilar (angle close to 90°), the cosine score draws near 0, signifying low relevance.
The conceptual translation of this into SEO is that the more similar the vectors (web pages) are, the smaller the angle between them, and hence the higher their cosine similarity. Consequently, these would be considered more relevant to each other, boosting their ranking during search queries.
Now, let's consider two query vectors where one has an angle of 30 degrees with a reference vector and the other an angle of 60 degrees. In this context, the cosine similarity measure for the first vector will be √3/2 (~0.87), and for the second vector, it would be 1/2 (0.5). Thus, even with a 30-degree difference, the cosine similarity value significantly drops, displaying that the second query is less similar to the reference vector.
What Is the Range of Values for Cosine Similarity, and What Do Values Close to 1 or -1 Indicate?
Cosine similarity, a common mathematical measurement often utilized in various forms of data analytics including Search Engine Optimization (SEO), is used to measure how similar two vectors or arrays of numbers are. Essentially, it measures the cosine of the angle between these two vectors projected onto multi-dimensional space. The range of values for cosine similarity extends from -1 to 1.
The value "1" implies that the vectors are identical, illustrating a perfect direct comparison. In SEO terms, a cosine similarity value close to 1 between two webpages could indicate that the content of those pages is extremely similar or even the same. This can be either good or bad depending on the context. It's ideal for pages within the same website to share some common topics or themes, contributing to the site’s overall coherency and relevance. However, it's also crucial for each page to have unique content to avoid penalties for duplications.
A cosine similarity value around "0" indicates vectors are orthogonal or decorrelated. In the context of SEO, this suggests that the webpages share very little common content or themes. It’s typical for this to occur naturally across a site covering a broad range of topics. It’s neither inherently good nor bad, but could be a cause for concern if two pages are expected to have related content but show low cosine similarity.
Conversely, a value of "-1" shows the vectors are diametrically opposed. In a data science environment, this implies that the two vectors being contrasted are moving in totally different directions. However, in an SEO context, this is practically impossible, as it would require one page to be the perfect opposite of another. Still, a particularly low negative cosine similarity could potentially indicate that the content of the two pages is at odds, possibly leading to confusion for both search engines and users.
Can Cosine Similarity Be Used for Text Data Analysis, and If So, How?
Certainly, Cosine Similarity is a potent mathematical method that can be effectively utilized for text data analysis, most prominently in the areas like Information Retrieval, Machine Learning, and SEO. It measures the cosine of the angle between two vectors to typify the degree of similarity between certain criteria respectively identified within these vectors. Now, let’s delve into how these diverse applications become feasible.
At the core of text data analysis stands the conversion of discrete words into numerical vectors. This is performed through sets, bags of words, or ensembles of n-grams. These models consider documents as a mere collection of individual words disregarding the syntax, and then convert them into high dimensional vectors. Each dimension corresponds to a unique word in all documents combined, and the magnitude of a vector along that dimension is dictated by that word's frequency within the respective document. However, this frequency may be scaled, as in TF-IDF model to offset the significance of universally frequent words.
Subsequently, the similarity of two documents corresponds to the proximity of their vectors. In essence, if the vectors align perfectly (i.e., the angle between them equals zero), the cosine similarity is 1, indicating complete similarity. On the other hand, if the vectors are orthogonal to each other (i.e., the angle between them being 90 degrees), the cosine similarity is 0, denoting no similarity at all.
Having processed the raw data into manageable vectors, Cosine Similarity is invoked to retrieve the documents for a query, cluster texts into coherent groups, or classify a new document into pre-existing categories.
Cosine similarity is immensely effective in SEO. When a user inputs a search query, search engines like Google aim to present the most relevant documents. To this end, the query is transformed into a vector and the cosine similarity between this vector and all document vectors is calculated. The search algorithm then delivers the documents with the highest cosine similarity, which are consequently considered the most relevant to the query.
Regardless of the application, it is the broad suitability of cosine similarity to high-dimensional, sparse vectors that drive its widespread adoption in text data analysis. Even though an array of alternatives to cosine similarity exist, this approach deals remarkably well with both the immense dimensionality of word vectors and the sparsity resulting from the fact that any given document only contains a small subset of all words.
What Are the Potential Challenges or Limitations of Using Cosine Similarity in Certain Scenarios?
Cosine Similarity is a widely used technique in Search Engine Optimization (SEO) for measuring the similarity between two text documents. Despite its several advantages, there are potential challenges and limitations when using cosine similarity in certain scenarios.
One major limitation of cosine similarity is that it only considers the angle between two vectors, ignoring their magnitudes. As a result, a long page with many words can have the same importance as a short page with few words but similar content, which isn't typically ideal in SEO.
Another challenge is the inability of cosine similarity to handle meaning in complex linguistic scenarios. It relies on the Bag of Words (BoW) model, which only analyses a text's word frequency. Thus, the method generally fails to understand context, synonyms, antonyms, and semantics. Consider the phrase "I don't like dogs". A direct comparison would associate it more closely with "I like dogs" than "I love cats", which is an incorrect interpretation.
Cosine similarity is also susceptible to high-dimensionality issues in large data sets. As the dimension increases, the computation of cosine similarity becomes more time-consuming and inaccurate. Moreover, with high-dimensional vectors, cosine similarity can give misleading results because the angle between pairs of vectors often converges towards orthogonality (90 degrees).
Another limitation lies in treating every term with equal importance. Cosine similarity assumes that every word contributes equally to the meaning of the text. However, in practice, not all words carry the same value or impact. Some keywords may hold more relevance in SEO than others, making them more important in determining the similarity between documents.
Lastly, in many scenarios, perfect textual matches are needed for a high cosine similarity score, which isn't flexible in terms of data or language diversity. If a text is translated into different languages, or two documents use different synonyms, cosine similarity may result in a low similarity score, which may not reflect the actual semantic connection between those texts.
How Can One Preprocess Data to Improve the Effectiveness of Cosine Similarity in a Given Application?
Preprocessing data is an essential step when applying Cosine Similarity in a given application.
This is because raw data often contains unnecessary elements, missing values, noise, and other inconsistencies that may affect the data's relevance and your application’s ability to deliver accurate results; hence, ineffective SEO. To improve the effectiveness of Cosine Similarity, you can apply several data preprocessing methods.
1. Text Normalization: This process transforms text into a standard form. For example, words like "SEO" and "Search Engine Optimization" can be standardized to a single form to avoid redundancy. Text normalization includes lowercasing all the text to avoid duplicate words due to case differences. It’s also essential to remove special character and punctuation as Cosine Similarity only considers the angle between vectors and not their magnitude.
2. Stopword Removal: Some words carry little or no meaning in the context of your application. Terms such as "the", "is", and "in" are often excluded from the text processing to ensure the most critical features are available, aiding in achieving a better Cosine Similarity score.
3. Tokenization: This is the process of splitting text into individual words or terms (tokens), enabling the application to understand and analyze the text more effectively. Each token is then represented as a dimension in the vector space model.
4. Stemming and Lemmatization: Both processes reduce the inflected or derived words to their base or root form. For instance, the words "running," "runs," and "ran" might be reduced to "run." By doing so, we can mitigate the noise in the dataset while simultaneously improving the computation of Cosine Similarity.
5. Term Frequency-Inverse Document Frequency (TF-IDF): This is a statistical measure that evaluates a word's relevance in a document. TF-IDF increases proportionally to the number of times a word appears in the document but is offset by its frequency in the whole corpus. This technique assigns more weight to the less frequent words that could help distinguish a document from others.
6. Vectorization: This is the process where textual data is transformed into a form that can be understood by machine learning algorithms. The high-dimensional space created now has contextual features simplifying the process of calculating cosine similarity among different vectors.
7. Handling Synonyms and Homonyms: Use methods like WordNet to understand the semantic relevance of a word in the context of its usage, this aids in differentiating between similar words and correctly categorizing them.
Preprocessing data for applications leveraging Cosine Similarity is crucial in search engine optimization as it enhances the understanding of data, improves the precision of search queries and consequently boosts the effectiveness of Cosine Similarity. It’s essential to remember that the preprocessing techniques to apply are contingent on the kind of data, application, and the specific task at hand.
Are There Variations or Adaptations of Cosine Similarity That Are Commonly Used in Specific Domains or Industries?
Cosine similarity is a widely-used metric in various fields that compares the cosine of the angle between two vectors, each vector representing an object in multi-dimensional space. The cosine similarity is beneficial because it is less sensitive to the magnitude of the vectors and more focused on the direction, making it useful for text-mining and information retrieval applications. There are several adaptations and variations of cosine similarity that are specifically designed for different domains.
In the realm of Text Mining and Information Retrieval, a variation of cosine similarity called TF-IDF (Term Frequency-Inverse Document Frequency) is commonly used. TF-IDF is a modification of cosine similarity that takes into account the frequency of the terms in the documents. Instead of merely analyzing the angle between vectors, TF-IDF assigns importance to each term based on its frequency of occurrence in a document compared to its frequency in all documents. High frequency words in a specific document but rare in general (e.g., industry-specific jargon) would carry more significance, contributing more to the cosine similarity score.
In Recommender Systems, Adjusted Cosine Similarity is frequently used. The goal of this modification is to adjust for the fact that different users may have different rating scales. For example, in movie recommendation systems, one user might rate all movies highly, while another is more critical. To compare the movie preference patterns of two users correctly, the average rating for each user is subtracted from each of their ratings before computing cosine similarity.
In Image Processing, Structural Similarity Index (SSIM), is a popular variation. While cosine similarity defines similarity as the cosine of the angle between two vectors, SSIM defines similarity by comparing local patterns of pixel intensities that have been normalized for brightness and contrast. SSIM incorporates important perceptual phenomena, including both luminance masking and contrast masking terms.
In the field of Bioinformatics, the Tanimoto coefficient, or Jaccard index, is a well-known adaptation of cosine similarity. Instead of representing the data as vectors in the conventional sense, this variation represents the data (such as gene expression patterns) as sets (for example, the set of genes expressed in a given cell type) and computes similarity as the size of the intersection divided by the size of the union of the sets.
How Does Market Brew Use Cosine Similarity In Its Search Engine Model?
The concept of cosine similarity is central to Market Brew's search engine model, as it forms the basis of the Cosine Similarity Inspector Tool and AI Overviews Visualizer. As a mathematically grounded principle that determines the text similarity by measuring the cosine of the angle between two vectors, it helps understand how closely related two pieces of text are in a multi-dimensional space. By employing this principle, Market Brew can accurately model Google's AI Overviews.
The Cosine Similarity Inspector Tool in Market Brew fleshes out how Google and similar advanced search engines perceive your content from the Sentence-BERT (Bidirectional Encoder Representations from Transformers) perspective. The tool sheds light onto the text window scores, providing a transparent insight into how cosine similarity presents itself in the model. Utilizing this tool, Market Brew illustrates the relationship between different sets of text, which contributes significantly to its search engine model's precision and relevance.
An example of Market Brew's use of cosine similarity can be seen in action in its AI Overviews Visualizer. The AI Overviews Visualizer enables users to validate how RAG (Retrieval
Augmented Generation) style LLMs (Large Language Models) identify and recall text fragments from their database for display purposes. Cosine similarity enables this retrieval process. By comparing the similarity between the user's query and that of the indexed content fragments, the search engine efficiently pulls out the most relevant pieces of information.
This precision and efficiency are crucial in enhancing the user experience, as the AI Overviews Visualizer provides insightful glimpses into the search engine's content delivery choices based on cosine similarity. As user expectations of relevance and precision in search results grow ever-higher, the users tend to engage more with the content that aligns most closely with their search intent. By utilizing the cosine similarity in its search engine model, Market Brew meets these expectations head-on, providing an enhanced user experience.
Cosine Similarity is also used in many blended algorithms inside Market Brew. Google's heading vector algorithm, for instance, is part of Market Brew's model. In the Heading Vector algorithm, users can visualize what kinds of heading structures Google likes, and adjust their headings and structure appropriately.
The same can be said about META Title Similarity and others.
You can expect to encounter content creation tools grounded on this principle with features like
Google Centerpiece Annotation optimizer. These tools aim to maximize the SEO value of content by refining it to align more precisely with relevant search queries, a crucial aspect of modern digital marketing.
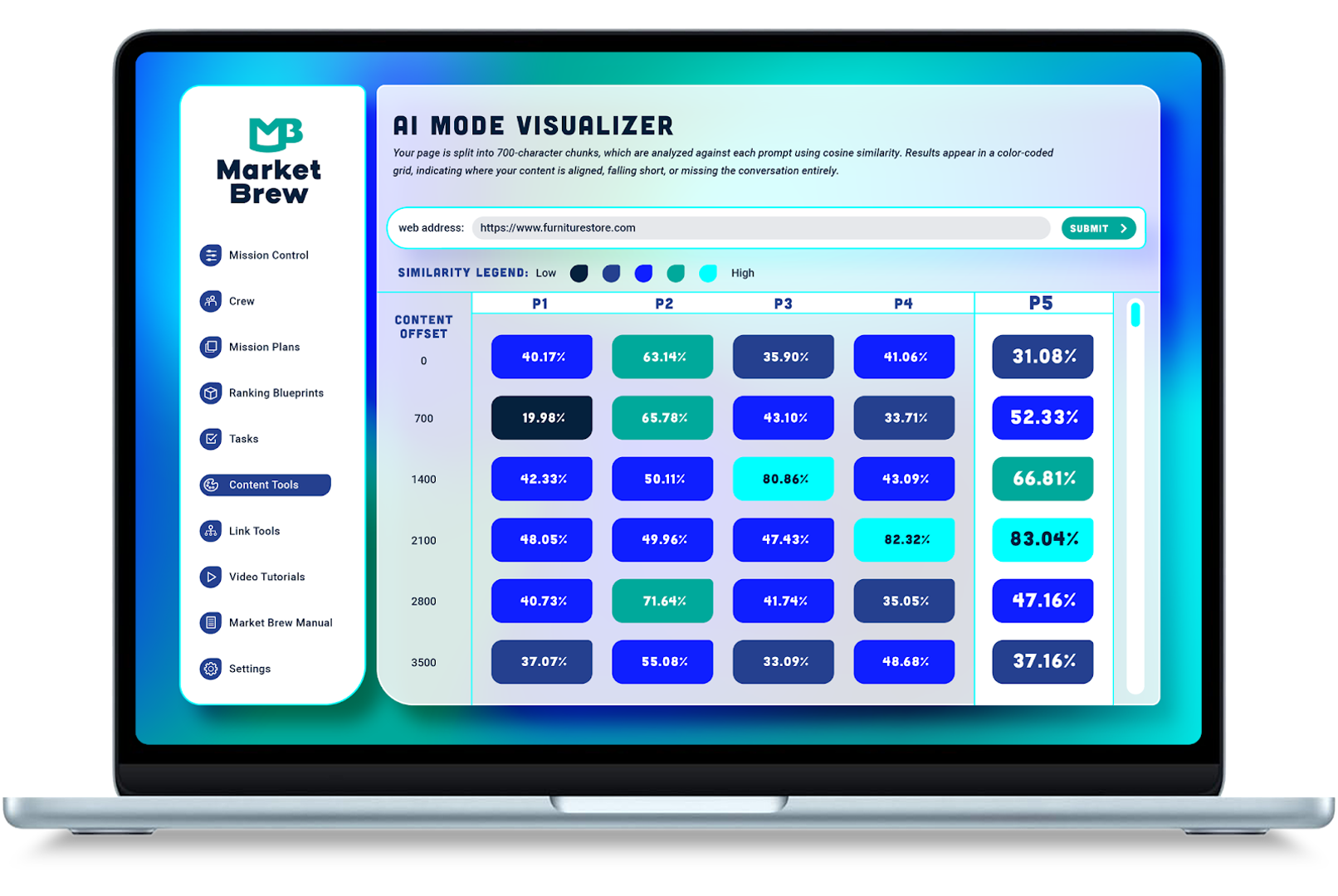
Market Brew incorporates cosine similarity into its search engine model by incorporating it into its Cosine Similarity Inspector Tool and AI Overviews Visualizer. These tools contribute significantly to the search engine model's precision, relevance, and overall user experience.
They also pave the way for future applications of cosine similarity in the field of content creation and optimization for enhanced SEO results.
If you want to understand how modern search engines are viewing your content, it is highly recommended to license Market Brew's search engine modeling software for your SEO team.
Ready to Take Control of Your SEO?
See how Market Brew's predictive SEO models and expert team can unlock new opportunities for your site. Get tailored insights on how we can help your business rise above the competition.
Schedule a demonstration today via our Menu Button and Contact Form to discover how we engineer SEO success.
You may also like
Guides & Videos
Convolution Neural Networks in SEO
Guides & Videos
Others
Lemmatization for Search Engine Optimization
Guides & Videos


